Question 1: Based on the family the graph below belongs to, which equation could represent the graph?
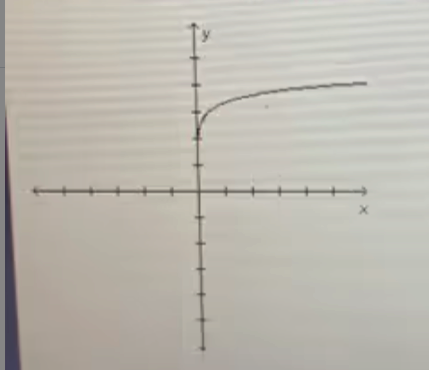
- y=2^x+3
- y=log (2x)+3
- y=2x^2+2
Answer: Based on the graph, the correct answer is y=log (2x)+3.
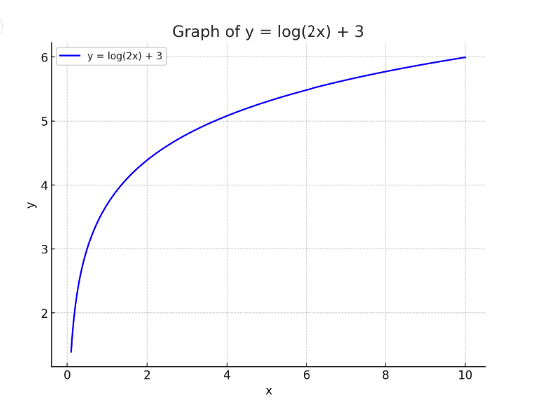
Graph of y=log (2x)+3:
Here is the graph of the equation y=log(2x)+3. The curve represents how the logarithmic function grows as x increases.
Question 2: Based on the family the graph below belongs to, which equation could represent the graph?
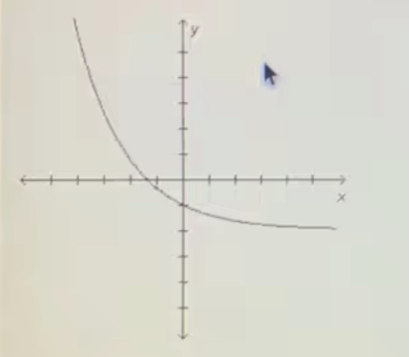
- y=0.6^x-2
- y=0.6x^2-1
- y=-0.6x^3-1
Answer: Based on the graph, the only correct answer is y=0.6^x-2.
Question 3: Based on the family the graph below belongs to, which equation could represent the graph
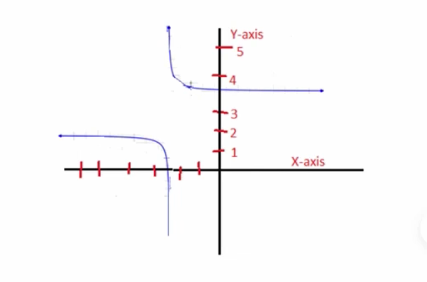
- y=(log x)+3
- y=(0.2)^x+3
- y=x^3+3
- y=1/(x+2)+3
Answer: Based on the graph, the only valid answer is y=1/(x+2)+3.
Explanation:
a. Incorrect option since the y-intercept of the graph is lies between 3 and 4 which does not match with the y-intercept of the given equation
b. Incorrect option since the y-intercept of the graph is lies between 3 and 4 which doest not match with the y intercept of the given equation
c. Incorrect option since the y intercept of the graph is lies between 3 and 4 which doest not match with the y intercept of the given equation
d. Correct option since every point on the graph satisfy the given equation

